The velocity of such on a transmission line is given as V = √(1/LC)
Where L = Line inductance per unit length (H/m) i.e Henry per meter
C = Line capacitance per unit length (f/m) i.e farad per meter
V = The velocity of propagation of surge (m/s) meter per seconds
Surge velocity is independent of size and spacing of conductor
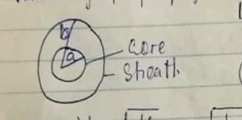
Velocity of propagation of surge in underground cable
Where a is the radius of the core
b is the radius of the sheath
C = 2πEo÷inB/A and L = μo/2π • inB/A
NOTE: E = Absolute permittivity of a medium
μ = Absolute permeability of a medium
E = EoEr and μ =μoμr
Eo = Absolute permittivity of free space and Er = relative absolute permittivity
μo = Absolute permeability of free space and μr = relative absolute permeability
For magnetic material V = √(1/LC)
V = √[1/(μo/2π • inB/A × 2πEo÷inB/A)
V = √(1/μoEo)
Eo = 4π × 10–⁷
μo = 1/36π × 10–⁹
V = √(1 ÷ (1/36π × 10–⁹ × 4π × 10–⁷)
V = √(1 ÷ (1/9 × 10–¹⁶ )
The 10–¹⁶ when the power leaves the numerator to the numerator it changes sign from 10–¹⁶ to 10¹⁶
V = √(1 ÷ 0.11 × 10¹⁶)
V = √9.009×10¹⁶
V = 3 × 10⁸m/s
One Comment