A string of suspension insulator consist of 3-units, the capacitance between each link pins to earth is one-sixth of the self-capacitance of the unit. If the maximum peak voltage per unit is not to exceed 20kv. Find the greatest working voltage and efficiency of the spring.
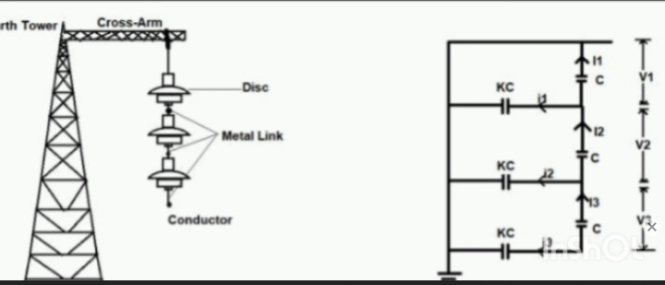
V = V1 + V2 + V3; = V1 + V2 + 20
Applying kcl(Kirchhoff’s voltage law) to NODE A
i3 + i1 + ic1
WC2V2 = WC1V1 + WCV1
WMCV3 = WMCV2 + WC(V1 + V2)
MV2 = MV1 + V1
MV2 = 7V1
M = C1/C ; C1 ÷ 1/6C1 = 6
6V2 = 7V1
V2 = 7/6V1
V3 = 20kv
AT NODE B
i3 = i2 + ic2
WC3V3 = WC2V2 + WC(V1 + V2)
Since M = C3/C, therefore C3 = MC
Therefore we’ve,
WMCV3 = WMCV2 + WC(V1 + V2)
Divide through by WC
MV3 = MV2 + V1 + V2
Recall, from the solving = 6
6V3 = 6V2 + V1 + V2
6V3 = 7V2 + V1
Recall V2 = 7/6V1
Therefore,
6V3 = 7V2 + V1
= ; 6V3 = 7/6 × 7V1 + V1
6V3 = 49/6V1 + V1
6V3 = 55/6 V1
Cross multiply
V3 = 55/36 × V1
V3 = 20kv
Therefore, 20kv = 55/36 × V1
V1 = (36×20kv) ÷ 55
V1 = 13kv
WC3V3 = WC2V2 + WC(V1 + V2)
Since M = C3/C, therefore C3 = MC
Therefore we’ve,
WMCV3 = WMCV2 + WC(V1 + V2)
Divide through by WC
MV3 = MV2 + V1 + V2
Recall, from the solving = 6
6V3 = 6V2 + V1 + V2
6V3 = 7V2 + V1
Recall V2 = 7/6V1
Therefore,
6V3 = 7V2 + V1
= ; 6V3 = 7/6 × 7V1 + V1
6V3 = 49/6V1 + V1
6V3 = 55/6 V1
Cross multiply
V3 = 55/36 × V1
V3 = 20kv
Therefore, 20kv = 55/36 × V1
V1 = (36×20kv) ÷ 55
V1 = 13kv
V2 = 7V1/6
7(13)/6 kv
= 15.2kv; approximately 15kv
Maximum voltage of the spring
V = V1 + V2 + V3
V = 13 + 15 + 20
V = 48kv
V = 13 + 15 + 20
V = 48kv
Maximum efficiency of the spring
Efficiency = V ÷ (n×V3) × 100
= (48kv) ÷ (3×20kv) × 100
48/60 × 100 = 80%
